Why Z Score?
We have already Empirical rule of normal distribution, that gives approximate percentile, but z score gives more accurate percentile
What is z Score?
A z Score (standard score / normalized score) this describes, how many standard deviations a specific data point is away from the mean of the data set.
It tells us that how much percentage a particular data point above the rest of data points
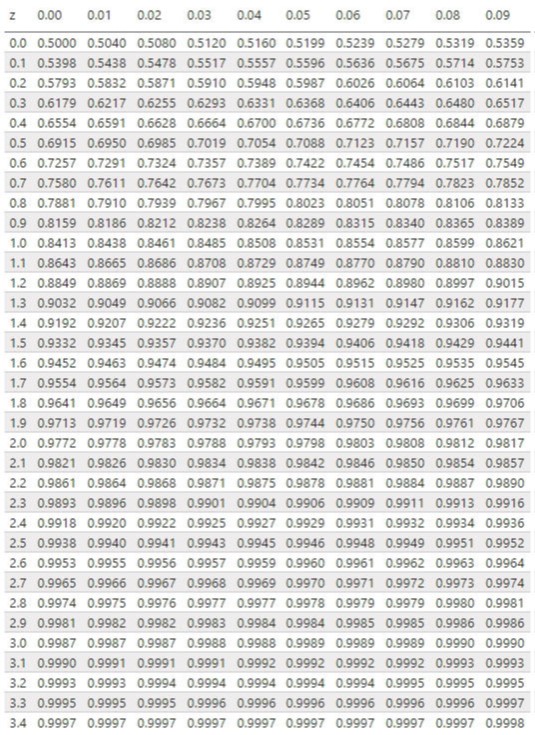
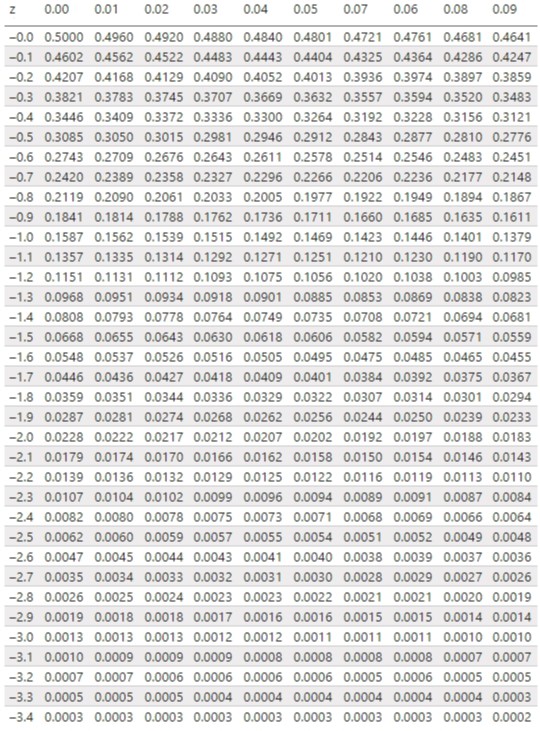
Calculate z Score:
z = (x – μ) / σ
- z is the z-score
- x represents the specific data point where wanted to calculate the z score
- μ (mu) is mean of the data set
- σ (sigma) represents the standard deviation of the data set
Interpreting z Scores:
- Positive z Score: A positive z Score indicates that the data point is above the mean
- Negative z Score: A negative z-score indicates that the data point is below the mean
z Score of 0: z-score of 0 signifies that the data point is exactly equal to the mean
Example:
Test score of 20 students in a subject,
Scores: 80, 75, 90, 85, 95, 78, 82, 100, 68, 88, 72, 89, 84, 79, 92, 87, 70, 98, 81, 76
Mean of all score is = μ = 83.5
Standard deviation = σ = 7.8
Marks of interest is 90 (user defined value, here we are taking 90 as an example)
So,
z = (x – μ) / σ
z = (90 – 83.5) / 7.8 = 0.83
So in conclusion, value form z table corresponding to 0.83 is 0.7967, we can say that student who have scored 90 marks is having 79.67 percentile
Z Score Table