Example 1
A store believes that new product has 100 sales per day compared to their old product. We want to test this claim statistically
Sample size = 10 stores = n, sample mean = 103 = x̄, Standard deviation given is 5 units per day = σ_population = 5
Null Hypothesis (H0): μ = 100; Number of new product sold per day is 100
Alternative Hypothesis (H1): μ ≠ 100; Number of new product sold per day is not 100
Alpha = 5% (95% confidence)
From, central limit theory, mean of sample distribution is distributed normally
Note:
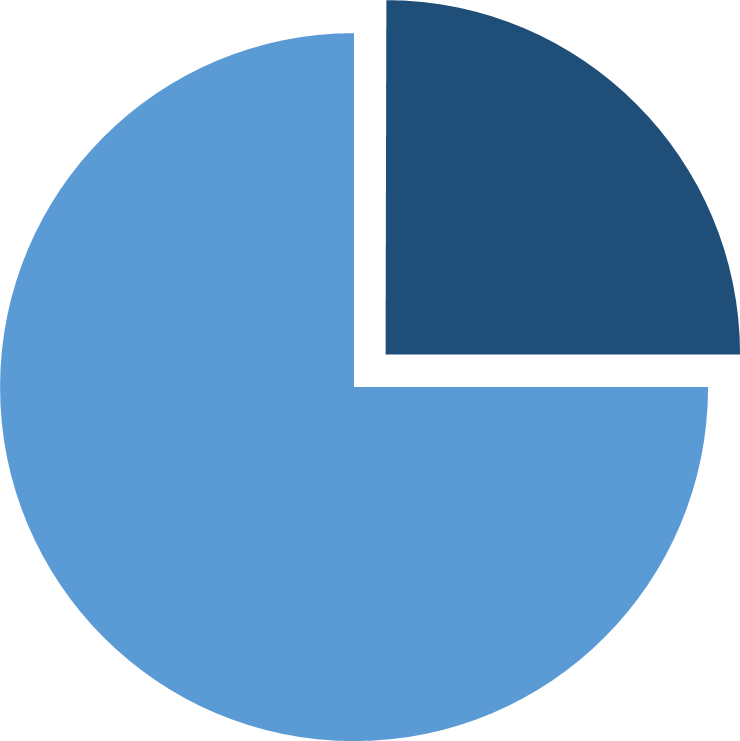
- This is 2 sided test because distribution is normal and values distribute equally because of symmetry, we might have to subtract p value from 100% to check critical region (p value from z score < alpha) because critical region is on right side of P( x̄ ≤ 103)
- In one sided test we could skip subtracting rom 100% because P values covers the area left side of x̄ in normal distribution
- One sided test hypothesis: H0: μ ≤ 103, H1: μ > 103 or H0: μ ≥ 103, H1: μ < 103
So lets calculate z score (because normal distribution)
z = (x – μ) / σ
σ_sample = σ_population / √n = 5/√10 = 3.16
z = (x̄ – μ) / σ_sample = ( 103 – 100 ) / 3.16 = 0.94
P value for z score 0.94 is 0.8264
P( x̄ ≤ 103) = 0.8264
In normal distribution all of the area which is less than 103 is totaling to 82.64%
If we take values to the right of 103 ie, 100% – 82.64% = 17.36% (because it is 2 sided test)
Lets check if P < Alpha;
Here P( x̄ ≤ 103) is greater than Alpha, 17.36% > 5%.
So, we are accepting null hypothesis and rejecting alternative hypothesis. Number of new product sold per day is 100
Note: Typically we usually don’t get population standard deviation in real life examples, such that we cannot calculate the σ_population and Z score. So we use Student T test to mitigate this type of problem
Example 2
Hypothesis proportion test example 2
Possible scenarios in proportion test
| Null Hypothesis (H0) | Alternate Hypothesis (H1) |
| H0: p= (2 side tail) | H1: p≠ (2 side tail) |
| H0: p≤ (1 side tail) | H1: p> (1 side tail) |
| H0: p≥ (1 side tail) | H1: p< (1 side tail) |
Suppose
H0: p≥ 25%
H1: p> 25%
n=400
s=91
p^ = s/n
p = p^ = 91/400 = 0.2275
σ_p = √( p *(1- p)/ √n
σ_p = √( 0.2275*(1- 0.2275)/ √400 = 0.0114
z= (x̄ – μ) / σ_p
z = (0.2275 – 0.25)/0.0114 = -1.97 => 0.0244(p value from z table_)
p value from z table= 0.0244
As we can see p < alpha, so we reject null hypothesis