Chebychev’s Theorem
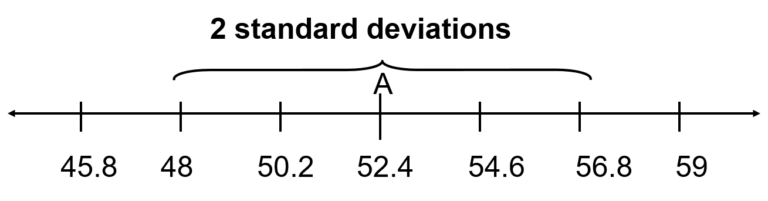
For any distribution regardless of shape the portion of data lying within k standard deviations (k > 1) of the mean is at least 1 – 1/(K^2) Eg: mean = 6, Standard deviation = 3.84 For k = 2, at…
Probability
Student’s T test
When Student’s T test should be used? Typically we usually don’t get population standard deviation in real life examples, such that we cannot calculate the standard deviation of population (σ_population) and Z score. So we use Student T test to…
Hypothesis test examples
Example 1 A store believes that new product has 100 sales per day compared to their old product. We want to test this claim statistically Sample size = 10 stores = n, sample mean = 103 = x̄, Standard deviation…
Confidence Interval and Margin of Error
Confidence Interval (CI): Range of values that is to contain the true population parameter (mean, proportion) with certain level of confidence Margin of Error (ME): Amount of uncertainty/ potential error our estimate or Confidence Interval Relationship between Confidence Interval and…
Hypothesis?
Hypothesis is an educated guess or a tentative statement about the relationship between two or more variables Types of Hypothesis: Note: We are collecting enough evidence to say that hypothesis to accept or reject the hypothesis How Hypothesis works? Note:…
Poisson distribution
Poisson distribution focuses on the number of events occurring in a specific interval (time, space, etc.) One parameter (λ) represents the average rate of events occurring within the interval, it will be the expected value from experiment Poisson distribution deals…
Binomial distribution
Probability distribution that describes the likelihood of getting a certain number of successes in a fixed number of independent trials, each with only two possible outcomes: success and failure We calculate the probability of getting a specific number of successes…
Central limit theorem
Central limit theorem describes the behavior of the sampling distribution of the mean of a random variable, It allows to make inferences about populations based on samples, distributions of sample means approaches normal distributions, even when the original experiment doesn’t…
Law of large numbers in probability
Suppose, we are calculating sample mean, as the number of samples increases the output accuracy increases, this theory says that as the samples/iterations/trials approach infinity we get most accurate output Applications of law of large numbers
Expected value in probability theory
Expected value helps us find average value we can expect from an random event Formula: E = Σ(x * P(x)) Example: I roll a fair six-sided dice. What’s the expected value from the dice? There are six possible outcomes (1,…
